Big O Notation in Layman term

Hi Guys !!! Hope all is well.

In my previous post Data Structures for Android Developer, I have quoted below quote. 
Bad programmers worry about the code. Good programmers worry about data structures and their relationships — Linus Torvalds

So, What is Big O?

• Big O notation is the language we use for talking about how long an algorithm takes to run (time complexity) or how much memory is used by an algorithm (space complexity). 
• Big O notation can express the best, worst, and average-case running time of an algorithm.

Big-O as time complexity

•  Analysis of running times does not take certain things into account, such as the processor, the language, or the run-time environment. 
• Instead, we can think of time as the number of operations or steps it takes to complete a problem of size n.
• In other words, big O notation is a way to track how quickly the run-time grows relative to the size of the input
• In the worst-case, the question becomes this: What are the most operations/steps that could happen for an input of size n?

O(1) → Constant Time

O(1) means that it takes a constant time to run an algorithm, regardless of the size of the input.

In programming, a lot of operations are constant. Here are some examples:

• math operations
• accessing an array via the index
• accessing a hash via the key
• pushing and popping on a stack
• insertion and removal from a queue
• returning a value from a function

O(n) → Linear Time

• O(n) means that the run-time increases at the same pace as the input
• In programming, one of the most common linear-time operations is traversing an array
• Generally speaking (but not always), seeing a loop is a good indicator that the particular chunk of code you’re examining has a run time of O(n)

O(n²) → Quadratic Time

O(n²) means that the calculation runs in quadratic time, which is the squared size of the input data.
In programming, many of the more basic sorting algorithms have a worst-case run time of O(n²):

• Bubble Sort
• Insertion Sort
• Selection Sort

Generally speaking (but not always), seeing two nested loops is typically a good indicator that the piece of code you’re looking at has a run time of O(n²). Likewise — three nested loops would indicate a run time of O(n³)!

O(log n) → Logarithmic Time

O(log n) means that the running time grows in proportion to the logarithm of the input size. this means that the run time barely increases as you exponentially increase the input.

In programming, the act of searching a word through a physical dictionary is an example of a binary search operation — the most typical example used when discussing logarithmic run times.

O(n log n) → Linearithmic Time
which is often confused with O(log n), means that the running time of an algorithm is linearithmic, which is a combination of linear and logarithmic complexity. Sorting algorithms that utilize a divide and conquer strategy are linearithmic, such as the following:

• merge sort
• timsort
• heapsort

Calculating Big O
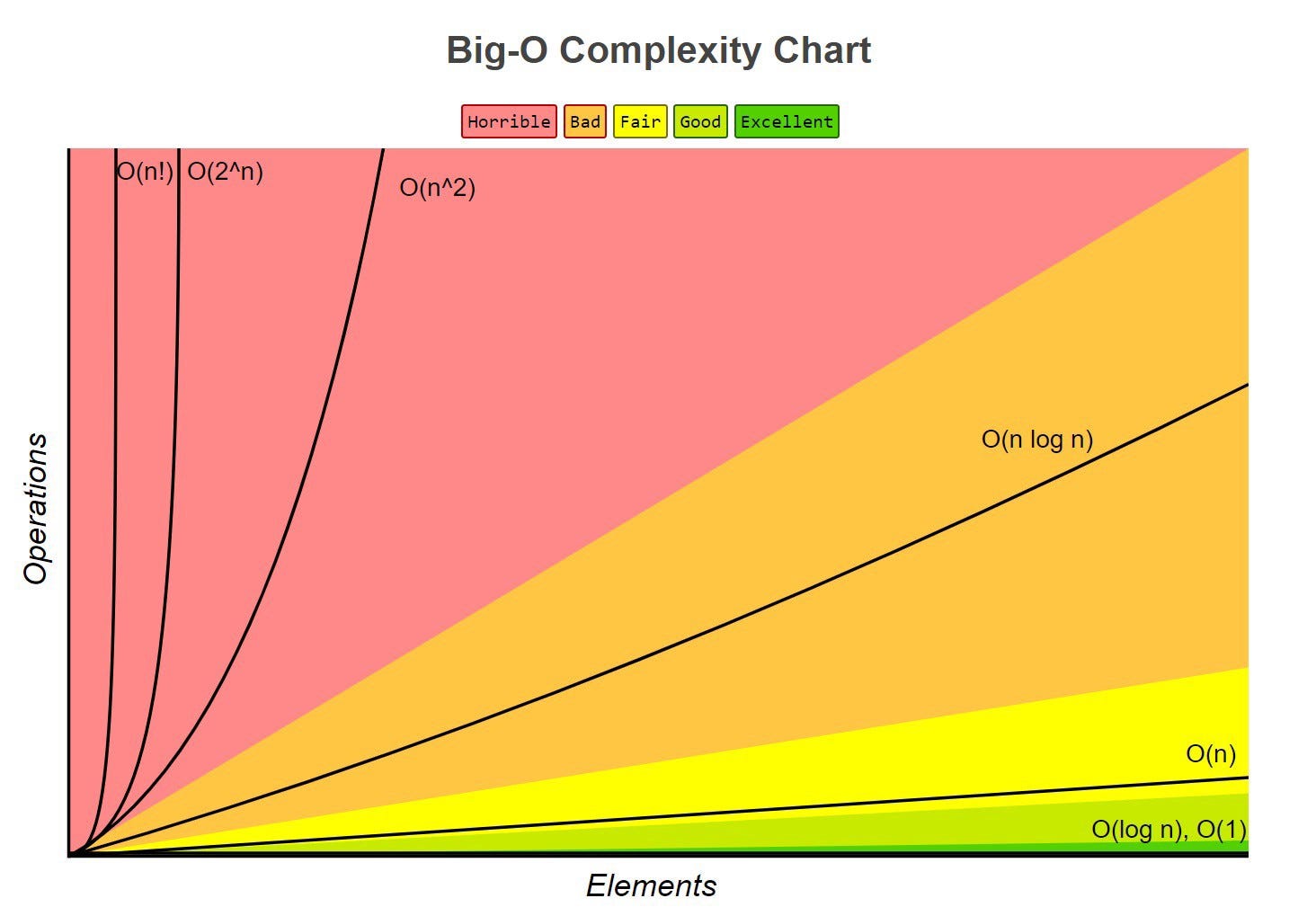
Thus far, we’ve only focused on talking about big O .

 How do we calculate big O if we are dealing with an algorithm that has several parts?

Below is the few point keep in mind  during calculation of Big O

• Assume the worst
• Remove constants
• Use different terms for inputs
• Drop any non dominants

1. Assume the worst
When calculating Big O, you always think about the worst case.
For example, if you were to loop over an array and look for an item, it could be the first item or it could be the last. As we aren’t certain then we must assume O(n) in this instance.

2. Remove constants
We could express the Big O notation of a function as O(1 + n/2 +100) but it’s really too specific. 

We can remove our O(1) operations because, as a rule of thumb, they are likely to be insignificant compared to our O(n) operations. 

If we are providing a million items in our input array, then an extra 100 operations from O(1) aren’t our main concern.
So then we have O(n / 2) — as n gets larger and larger, dividing it by two has a diminishing effect. So ultimately our Big O notation for this function becomes O(n).

3. Different terms for inputs
If we were to loop twice of the same array then our Big O is technically O(2n) but let’s drop the constants so we are left with O(n). 

But now we need to think about different terms for inputs. What does that mean?

if We have a function that take 2 diferent argument (long and int)
One could be one item long, the other could contain a million items. So our function is no longer O(n), it is O(a + b). The n we use in our notation is arbitrary, so we need to reflect both inputs in our notation.

4. Drop non-dominant terms
So we have a single loop at the top which is O(n) and then a nested loop which is O(n²). So our total is O(n + n²). But as we saw in rule #2, we want to drop constants. So which of the two terms is more important to us?
In this case we drop O(n) and retain O(n²) as this is more important. It is the dominant term as it has a much heavier impact on performance.

Thanks

Saurabh Sharma

Happy Coding !!!